1789. Order of a permutation
Find the order of a permutation p.
A permutation of n elements
is an ordered sequence of n distinct integers from 1 to n.
The order of a permutation p is
defined as the smallest positive integer k such that
pk = ε, where ε is the identity
permutation (1, 2, ..., n).
Input. The first line contains a positive integer n (0
< n ≤ 100), the size of the permutation p. The second
line contains the permutation p, represented as a sequence of n integers.
Output. Print the order of the given permutation.
|
Sample
input 1 |
Sample
output 1 |
64 3 2 5 1 6 |
6 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
94 3 6 8 9 7 2 1 5 |
12 |
SOLUTION
combinatorics - permutations
Algorithm analysis
Let p be a given
permutation, and let p[i] denote the element of the
permutation located at position i. Consider the sequence of elements: i, p[i], p[p[i]], … . Since the number of elements in the
permutation is finite, there exists a smallest k such that p[i]k = i.
The sequence
of elements i, p[i], p[p[i]], …, p[i]k-1, where p[i]k = i, is called a cycle. The length
of the cycle is k.
Any permutation can be
represented as a list of cycles. For example, the permutation [4, 3, 2, 5, 1,
6] can be represented as (1, 4, 5)(2, 3)(6).
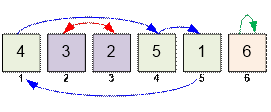
For example, the sequence (1, p[1],
p[p[1]]) = (1, 4, 5) forms a cycle because p[p[p[1]]]
= p[1]3 = 1. The length of this cycle is 3.
The order of a permutation is the
least common multiple (LCM) of the lengths of its cycles.
Example
In the first example, the
permutation [4, 3, 2, 5, 1, 6] is represented as (1, 4, 5)(2,
3)(6). The
lengths of the cycles are 3, 2 and 1. The order of the permutation is LCM (3, 2, 1) = 6.
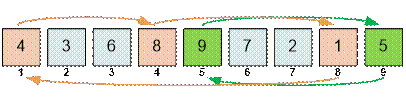
In the second example, the
permutation [4, 3, 6, 8, 9, 7, 2, 1, 5] is represented as (1, 4, 8)(2, 3, 6, 7)(5, 9). The lengths of the cycles
are 3, 4 and 2. The order of the permutation is LCM(3, 4, 2) = 12.
Algorithm implementation
The array p stores the input permutation. The array used is used to mark processed
elements.
#define MAX 101
int p[MAX], used[MAX];
Read the input permutation.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&p[i]);
The
variable res is used to compute the order of the permutation p.
res = 1;
memset(used, 0, sizeof(used));
Iterate
over the indices of the permutation. For each processed index i, set used[i]
= 1.
for (i = 1; i <= n; i++)
if (!used[i])
{
The cycle
with the element p[i] is not found yet. Search for the length of the cycle len in the permutation, starting from index j = i. To do this, consecutively move through the
indices j, p[j], p[p[j]], …, until we encounter an already processed element. All
visited indices j are marked as visited by
setting used[j]
= 1.
len = 0;
j = i;
while (!used[j])
{
used[j] = 1;
j = p[j];
len++;
}
The
variable len contains the length of the current cycle found. Compute the
LCM of the lengths of all cycles.
res = lcm(res, len);
}
Print the answer.
printf("%d\n", res);